La statistique étudie certaines caractéristiques : caractères ou variables d'un ensemble fini appelé population. Les éléments de cette population étudiée sont appelés individus. Une variable peut être :

• Quantitative : numérique et fait l'objet de calcul  ( âge, taille, poids, notes, nombres d'heures etc ...)
• Qualitative : c'est le contraire de quantitative, mais la variable peut très bien être numérique.
• Discrète:si la variable ne prend qu'un nombre fini de valeurs (ces valeurs sont notées x_i ) .
• Continue:si la variable prend ses valeurs dans un intervalle (classe )

L'effectif total est la somme des effectifs de toutes les classes.
On le note souvent N, on a alors : N = n₁ + n₂ + n₃ + n₄ + n₅ = 50 .

Autre notation :

Dans le cas d'une série statistique continue, la classe modale est la classe du plus grand effectif : Exemple:
	Sur cette exemple, la classe modale est donc Classe modale ? [0;5[ [5;8[ [8;12[ [12;15[ [15;20]
Dans le cas d'une série statistique discrète, le mode est la valeur de plus grand effectif :
	mode ? aucun 8 9 10 8-9-12 11 8-12-13 12

Moyenne

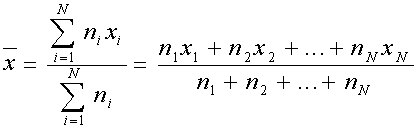n1, n2, n3, .........,nN sont les effectifs correspondants aux variables x1, x2, x3, .........,xN., si la série est discrète ou aux centres de classe x1, x2, x3, .........,xN., si la série est continue.
Exemple:
Série discrète	Série continue
Médiane La médiane est un paramètre de position, qui permet de couper la population étudiée en deux groupes contenant le même nombre d'individus. Ce paramètre est utile pour donner la répartition du caractère étudié, car 50 % environ de la population étudiée a une modalité inférieure à la médiane et 50 % une modalité supérieure à la médiane. Exemple On fait une étude statistique sur les 50 notes attribuées par un jury à un examen, voici les résultats obtenus en classant ces notes par ordre croissant. Variable discrète Utilisons la colonne des effectifs cumulés pour déterminer la médiane : il y a 50 notes, la  25ème note est 9 et la 26ème : 10. 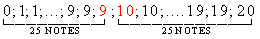Voici la répartition des notes : Dans le tableau il n'y a pas de valeur partageant la série statistique en deux groupe de même effectif , ( l'effectif total est pair ) dans ce cas l'intervalle médian est [9;10] et on prend pour médiane le centre de cet intervalle : 9,5 Variable continue Si la variable est continue ( regroupement par intervalle des résultats )  le calcul de la médiane se fait autrement : Utilisons la colonne des effectifs cumulés pour déterminer la médiane : Il y a 50 notes, 50 % de l'effectif total c'est 25, la médiane est ici la note correspondant à l'effectif cumulé 25. D'après la colonne "effectif cumulé" : 18 personnes  ont moins de 8 30 personnes ont moins de 12 La médiane se trouve donc dans l'intervalle [8;12[ ( appelé classe médiane ). Quartiles Les 3 quartiles sont les 3 valeurs qui partagent la population totale en 3 parteies d'effectifs égaux: Le 1er quartile Q1 correspond à 25 % de l'effectif total Le 2ème quartile Q2 correspond à la médiane, soit 50 % de l'effectif total Le 3ème quartile Q3 correspond à 75 % de l'effectif total

Indicateurs de dispersion

Etendue d'une série statistique

L'étendue d'une série statistique est la différence entre la plus grande et la plus petite valeur du caractère.
Exemple:
20 - 0 = 20,  20 est l'étendue de ces deux séries ( continue et discrète )

Variance et écart type

Pour calculer la variance d'une série statistique on utilise la formule :
Pour calculer la variance , il faut  calculer d'abord la moyenne. La variance peut être calculée aussi en utilisant la formule :
Ecart-type: L'écart-type est le nombre noté tel que : .

Ecart inter-quartile:

L'écart interquartile est égal à Q3 - Q1